ComputerVision

计算机视觉（2）数字图像与卷积

Table of content
  1. 1. 数字图像
  2. 2. 图像处理就是一种变换（transform）
  3. 3. 降噪
    1. 3.1. 多图像
    2. 3.2. 单张图片
  4. 4. 卷积
    1. 4.1. 一维数据卷积
    2. 4.2. 二维数据卷积
  5. 5. 图像模糊（blurring）
  6. 6. 边缘检测
    1. 6.1. Sobel边缘算子

数字图像

灰度图像

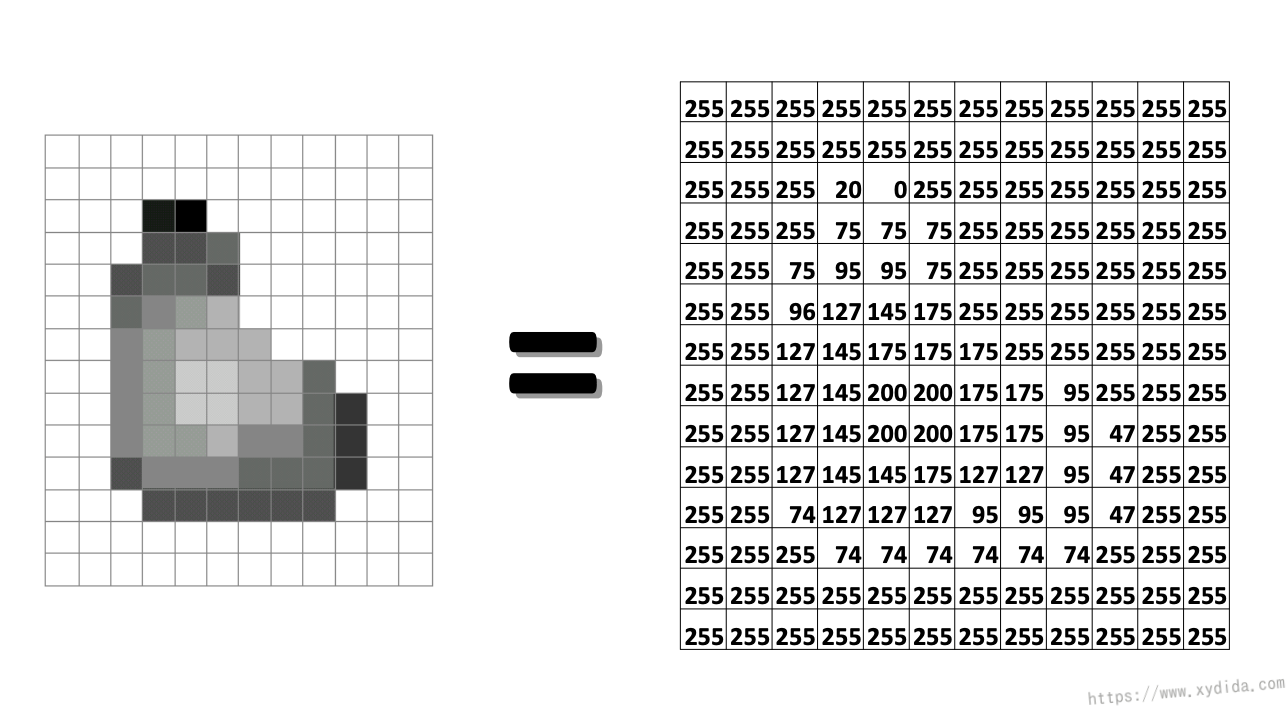
计算机视觉的主要任务就是分析数字图像，计算机中图像是以像素的形式构成方形的光栅（raster），常见的8位深度的图像中，0代表黑色，255代表白色，如上图是一张8位深度的灰度图（greyscale），可以将一个光栅图看作一个函数f(x,y)，参数为横纵坐标，输出结果就是像素的值即强度。

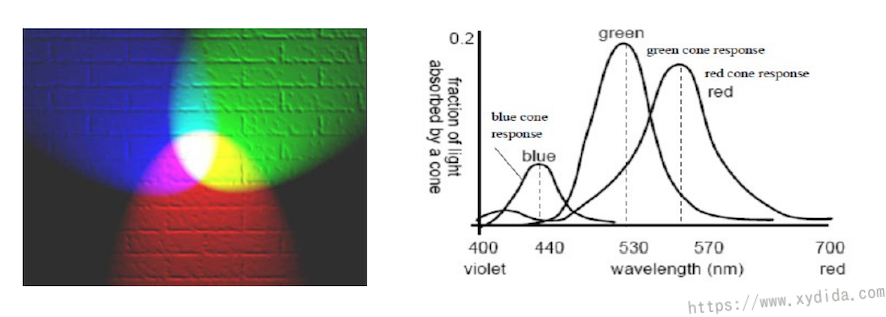
三个光栅构成彩色图像，其中光栅也称为通道，分别是红（Red），绿（Green），蓝（Blue）。

彩色图像

可以使用如下公式将RGB图像转换成Greyscale图像：

Y=0.3(R)+0.59(G)+0.11(B)Y = 0.3(R) + 0.59(G) + 0.11(B)

从公式中，各部分的洗漱代表了人眼对三种颜色的响应，绿光和红光相同的强度下，人眼会感觉绿色更亮一点，差不多是红色的2倍。上述转换使用Matlab代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
image = imread('pic.jpg');
// 分别显示不同的通道
// R
imgshow(image(:,:,1));
// G
imgshow(image(:,:,2));
// B
imgshow(image(:,:,3));

// 转换
grey = 0.3 * image(:,:,1) + 0.59 * image(:,:,2) + 0.11 * image(:,:,3);

imgshow(grey);

图像处理就是一种变换（transform）

图像处理任务可以看作是将原有的f(x,y)变换成新的函数g(x,y)的过程，比较常用的就是线性变换，如下图：

线性变换有如下优点：

  • 实用，可以检测边缘，细节锐化，降噪等
  • 配合卷积算子，效率高

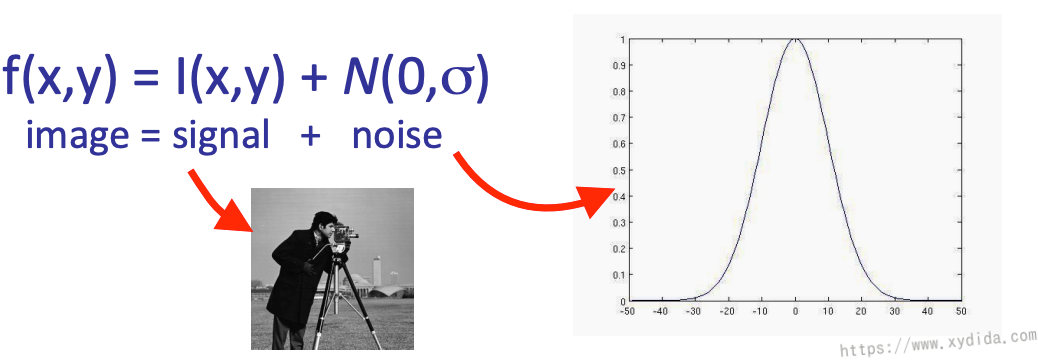
图像降噪是线性过滤器最常见的应用之一，图像的噪点类型多样，常见的"speckling"是一种热噪声，也是高斯噪声的一种，一些廉价相机在低光环境下拍出的照片通常都会有这种噪声。

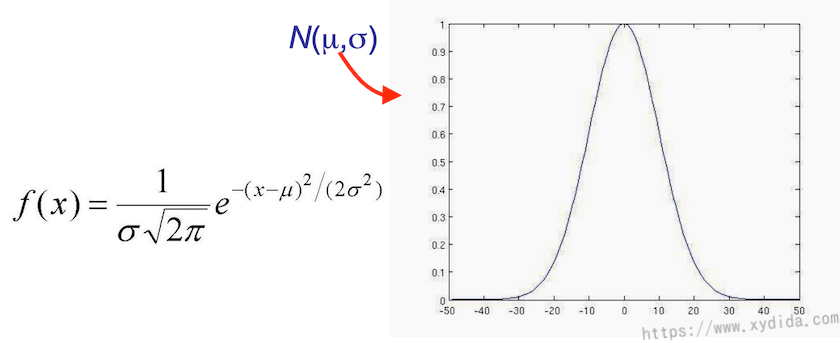
高斯噪声可以想象成在原始像素值上多加上一点，噪声值的分布是一个高斯分布，如下图，均值为0，标准差为10。

降噪

多图像

如果我们将相机固定在一个位置，拍了n张一样的图，但由于一些细微因素的影响，这n张图片的像素值不可能完全一样，因为一张图片的生成包含了原始图像信号和噪声信号：

平均法是将这n张图片的每个像素值取平均，最终得到一张更清晰的图像，由于高斯噪声的均值是0，所以当照片的数量越多，n越大，平均后得到的噪声就越小，如下图：

此方法需要很多张图像来获得好的效果，卫星拍照领域广泛使用，但平时生活中使用较少。

单张图片

正常情况下，只有一张带有噪声的图片，由于空间连贯性（spatial coherence），相邻像素强度是类似的，可以将像素分组，使用滑动窗口在每一组内取平均作为新的像素值，也可以起到去噪的效果，如下图：

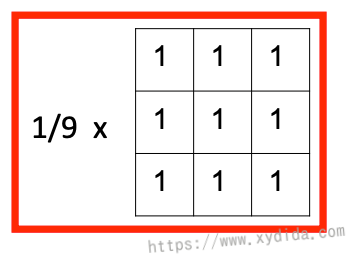
一种高效的组内平均方法是使用卷积算子，如果滑动窗口大小为3x3，则卷积算子如下：

操作起来就是将算子的每一个元素与窗口内对应的元素相乘，最后相加后结果四舍五入：

1/9∗(1∗0+1∗4+1∗0...)=4/9=01/9 * (1*0 + 1*4 + 1*0 ...) = 4/9 = 0

卷积

上面的例子可以知道，我们通过一个卷积算子能将图像f(x,y)转换成g(x,y)，通过线性组合周围像素的方式就叫做线性过滤，卷积算子的每个元素为对应像素的权重。

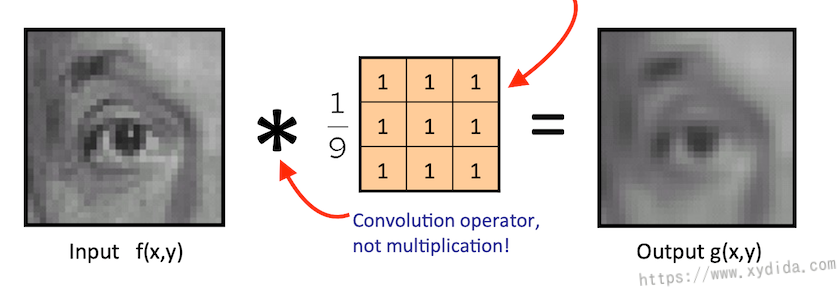
不同的算子权重可以创建处不同效果的图像，上例中每个权重都是1/9即取周围9个像素像素的均值，最后生成的图片更加模糊。下面是带有不同权重的算子：

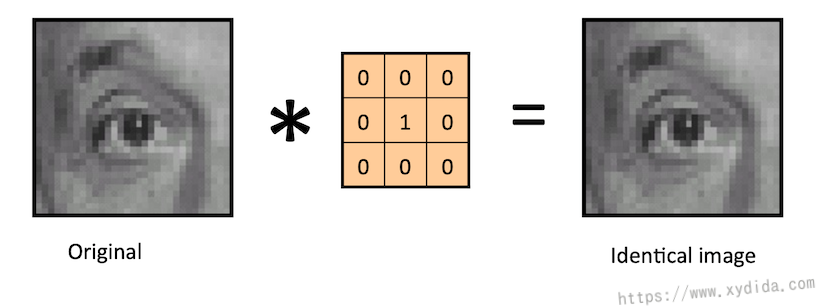
结果和原始图像一样：

图片向左移动一个像素：

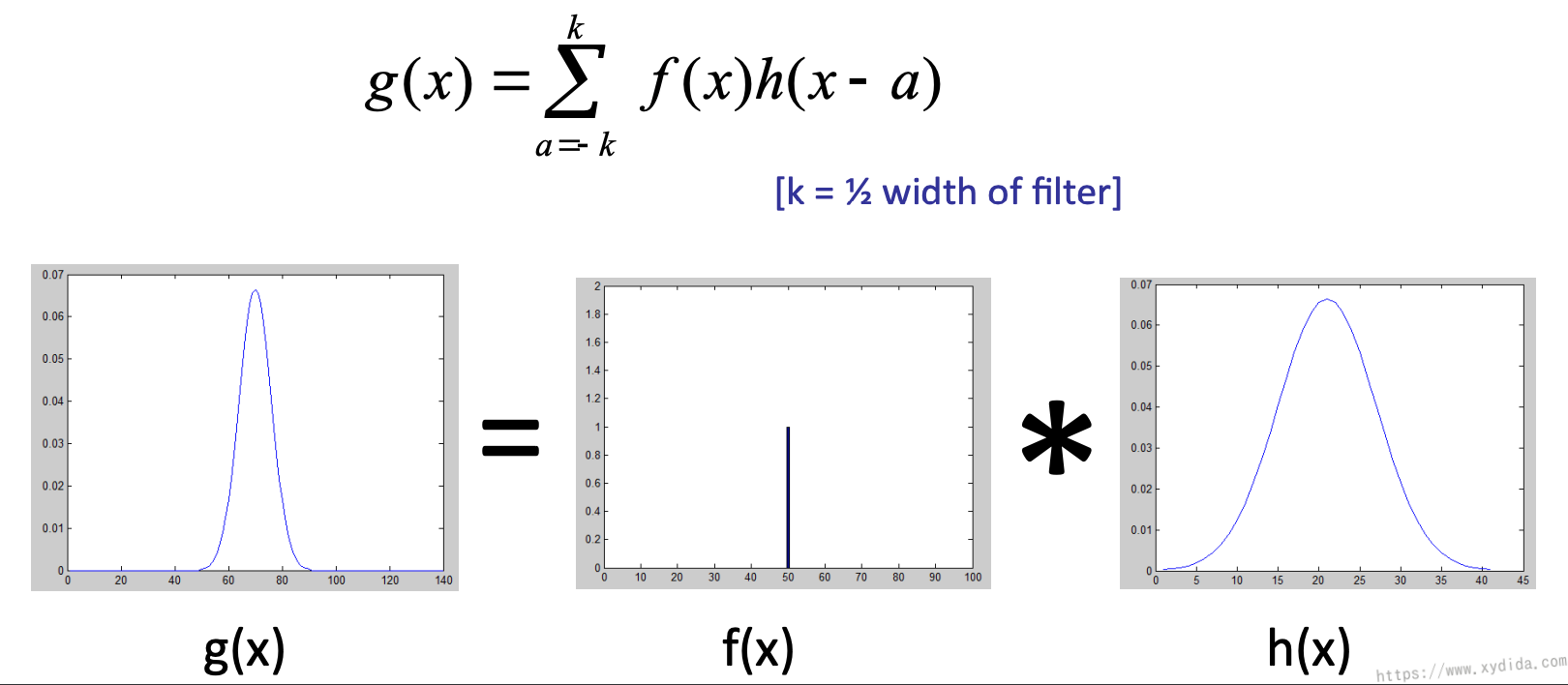
一维数据卷积

f(x)为输入信号，h(x)为过滤器：

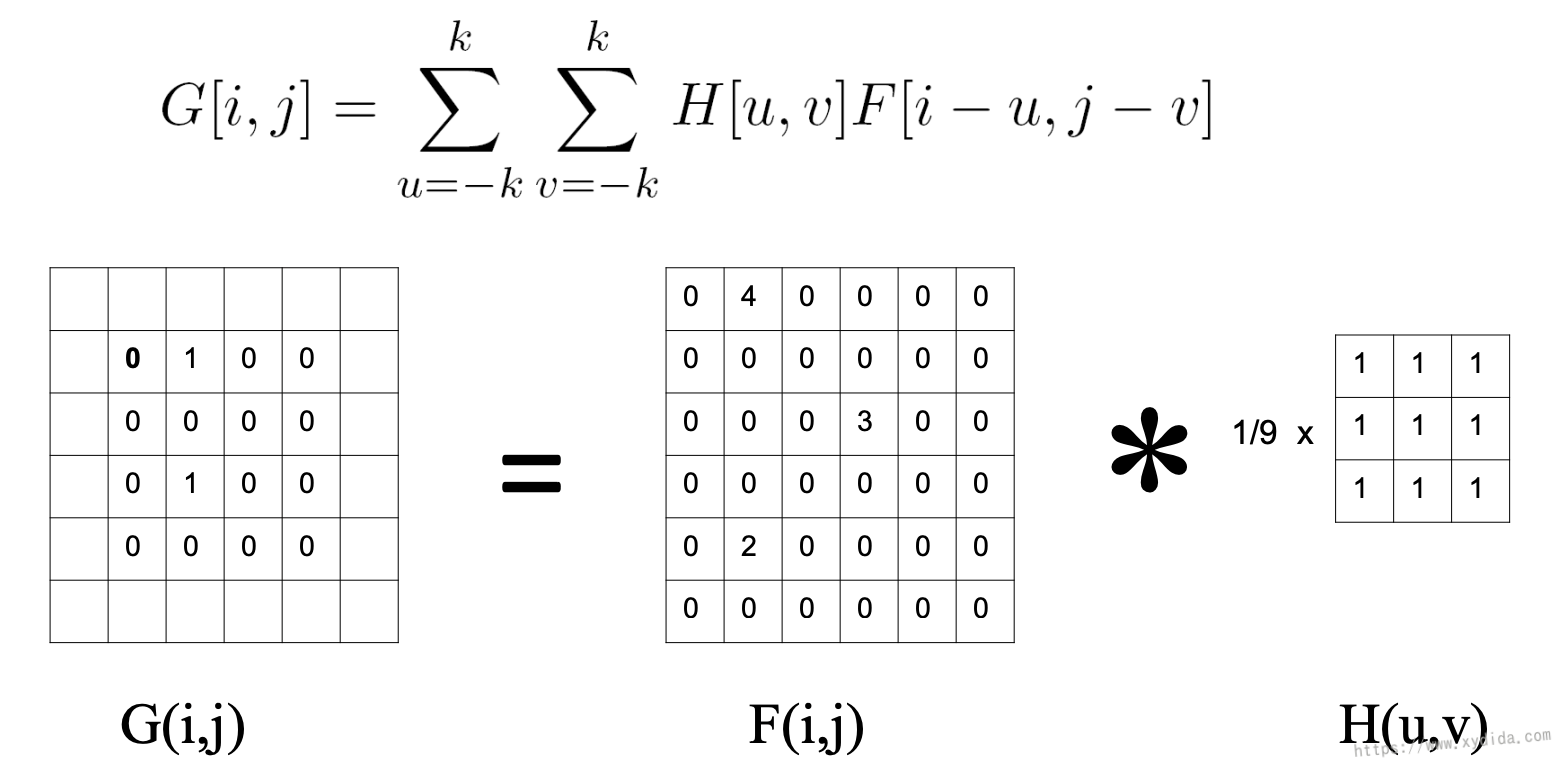
二维数据卷积

图像模糊（blurring）

上面图像去噪的例子中，是采用平均周围像素的方式，每个算子的大小都是一样的，又称作“Box filter”，可视化如下图：

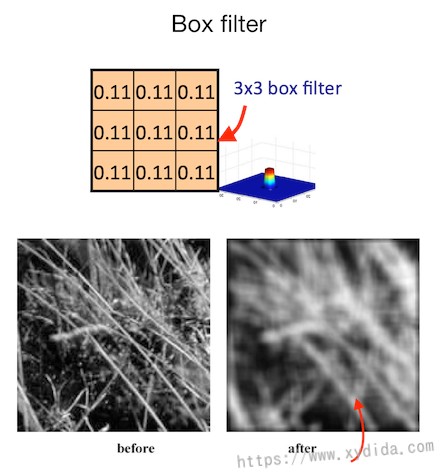
Box filter

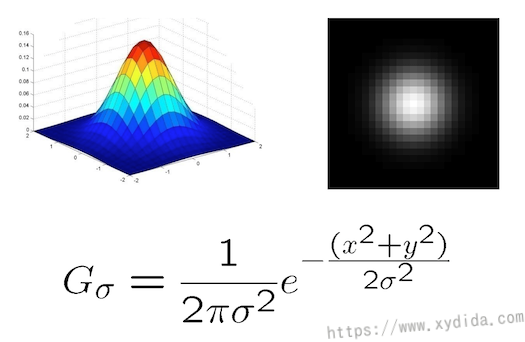
从结果来看，虽然是模糊的，但是图像不够顺滑，细看像一块一块的方块组成。如果换成使用高斯函数生成算子权重，即中间权重大，周围权重小，则结果会很平滑：

Gaussian filter

高斯算子通过高斯函数生成，选择一个固定的标准差，参数x,y为距离中心点的偏移量，离中心的越远，生成的权重越小，因为spatial coherence的原因，距离越远，相关性就越小，

Gaussian filter

边缘检测

线性过滤器也可以用于边缘检测，在图像中，边缘发生在强度不连续的地方，可以使用高通过滤器（high pass filter）来检测。

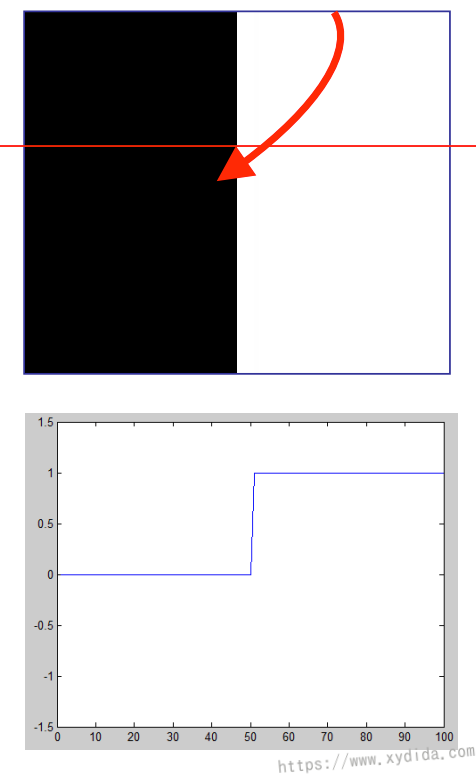
如上图，黑白中间即边所在，下面的强度图可以看到由黑到白时，强度发生了巨大的跳变，但是真实的图像中，这种变化往往不会这么明显，会稍微柔和一点。边缘分为水平和垂直方向，水平方向变化的边需要计算水平梯度（gradient），反之需要计算垂直梯度，图像梯度指向强度变化最快的方向。

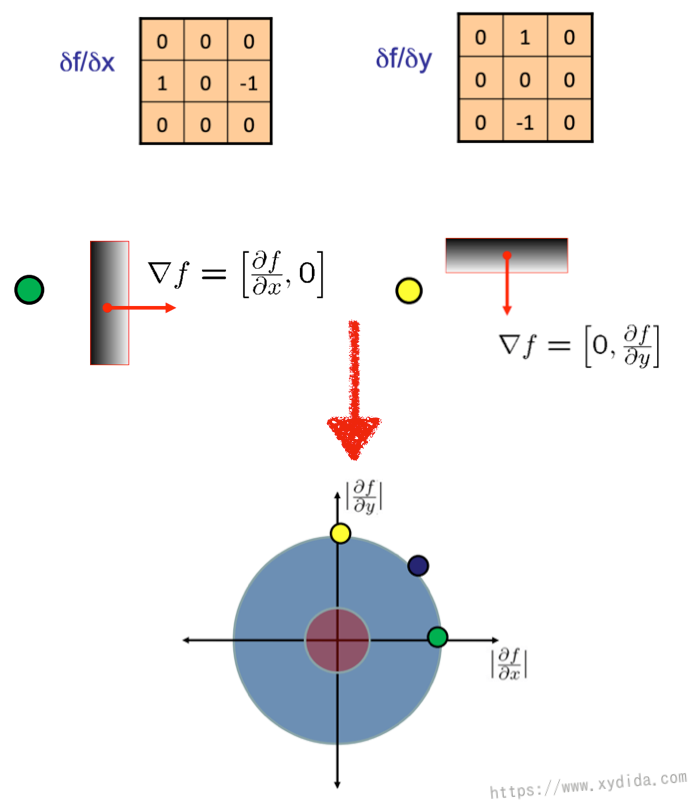
图像梯度强度

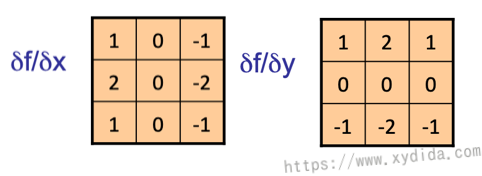
边又两个属性，分别是图像梯度和方向，可以分别通过公式1和公式2计算出来：

∥∇f∥=(δfδx)2+(δfδy)2(1)\lVert\nabla{f}\rVert = \sqrt{(\frac{\delta{f}}{\delta{x}})^{2} + (\frac{\delta{f}}{\delta{y}})^{2}} \tag{1}

θ=tan−1(δfδy/δfδx)(2)\theta = tan^{-1}(\frac{\delta{f}}{\delta{y}} / \frac{\delta{f}}{\delta{x}}) \tag{2}

如下，是一只老虎的梯度图：

Sobel边缘算子

Sobel经常被用来检测边缘，同时它还有平滑图像的功能，算子如下：