本地部署stable-diffusion-webui时,首次执行webui会需要安装各种依赖包,限于国内网络原因,安装会各种报错,比如会提示Couldn't install gfpgan错误,解决方法如下:
- 用编辑器打开webui项目根目录下的
launch.py文件 - 找到
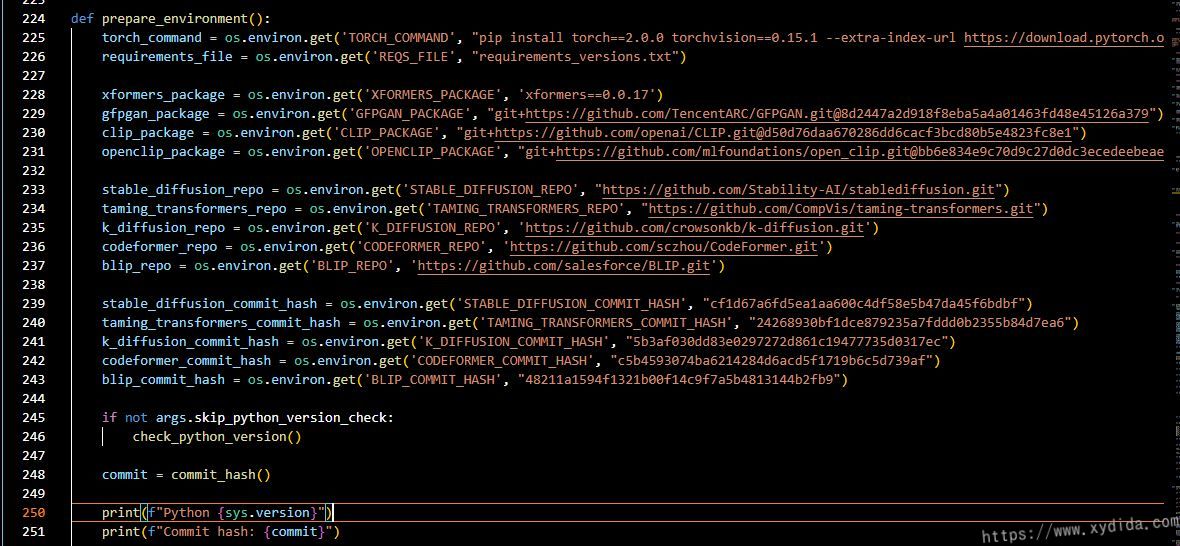
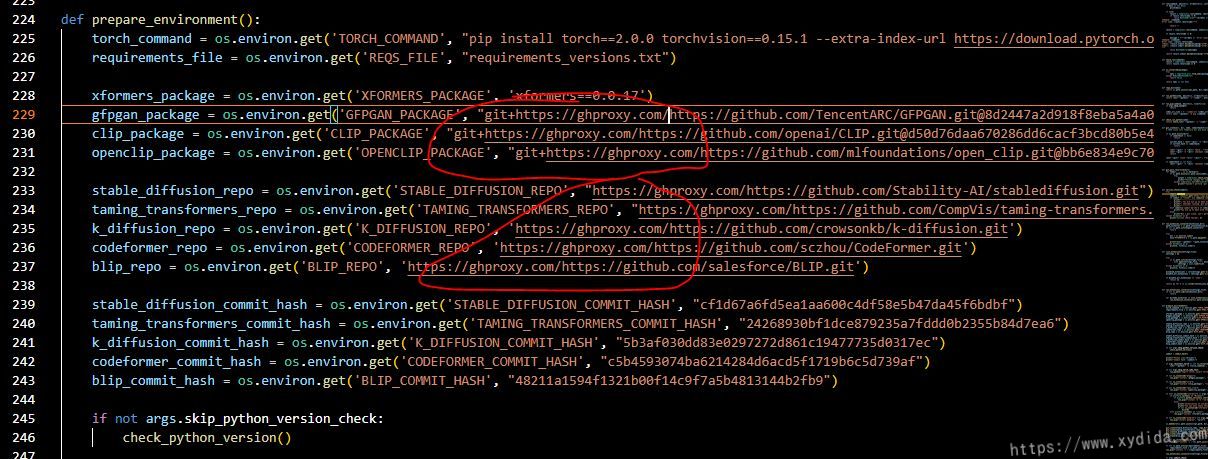
def prepare_enviroment()方法定义,大概在224行,修改里面的https://github.com/开头的链接,在这些链接前加上https://ghproxy.com/,最后修改如下:
最后,放一张用webUI跑的第一张图:

参考: