关于对比度
在图像中,对比度指明暗程度,对比度高说明物体相对于其他更容易分辨。如下图,左边低对比度图像看起来雾蒙蒙的,像是在阴天拍的,很难区分其中的细节,而右边高对比度图像就好像在夏天拍的,光线充足,看得很清楚。

Image thresholding is a process for separating the foreground and background of the image. There are lots of methods for image thresholding, Otsu method is one of the methods proposed by Nobuyuki Otsu. The Otsu algorithm is a variance-based way to automatically find a threshold value by which the weighted variance between foreground and background is the least.
With different threshold value, the pixel values of foreground and background are various. Hence, both pixels have different variance for different thresholding. The key of Otsu algorithm is to calculate the total variance from the two variances of both distributions. The process needs to iterate through all the possible threshold vlaues and find a threshold that makes the total variance is smallest.
The topic of my Msc dissertation is “Investigating AI and Digital Pathology” which mainly uses the Deep Learning to detect mitosis. This post I will introduce the techniques of the Digital Pathology.
Cancer is one of the main causes of deaths impacting not only human but also animals. This diagnosis of cancer is based on the histological slides of the body tissues. In the traditional pathology, microscope is used as a major tool to review the tissues on the physical glass slides. The analysis of the histological images is usually performed by the pathologists which is an exhaust and tedious task. Digital pathology is a sub-field of the pathology that converts the traditional slides into the digitalized images.
Training a deep learning model is a complicated task which not only needs to adjust the parameters such as learning, but also needs to process the training data. Normalized the data is one usefule approach and has been widely used for preparing dataset.
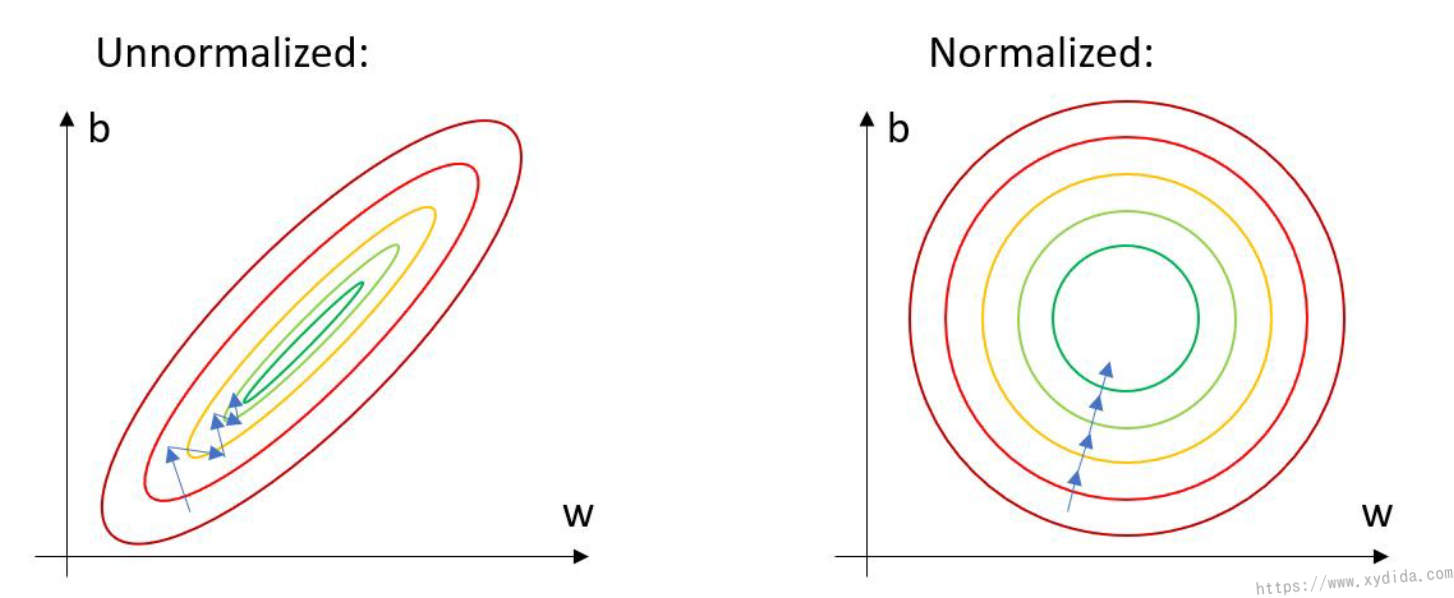
In deep learning, the image data is normalized by the mean and stadard deviation. This helps get consistent results when applying a model to new images. Hence, the convergence of the model

OpenSlide is a C library that provides simple interfaces to process Whole-Slide-Images (also known as virtual slides). WSIs are very high resolution images used in digital pathology. These images usually have several gigabytes and can not be easily read with standard tools or libraries because the uncompressed images often occupy tens of gigabytes which consume huge of RAM. WSI is scanned with multi-resolution, while OpenSlide can support read a small amount of image data at the resolution closest to a specifical magnification level.
OpenSlide supports many popular WSI format:
Although it is written by C, Python and Java bindings are also provided, and some other bindings are contributed in the Github such as Ruby, Rust.