前面的文章:
本文将介绍图像中的模式以及模式分类,并介绍机器学习中相关的理论基础,包括监督式分类,非监督式分类,overfitting,underfitting等。
机器学习Machine Learning
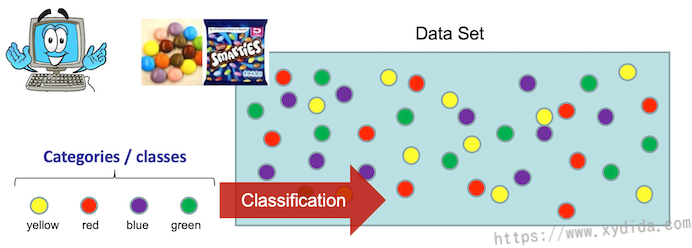
什么是机器学习?机器学习的是什么?以分类问题举例,一个袋子中装有不同颜色的球,它们除颜色外都相同,那我们在区分这些球时,只能根据颜色来区分,其它的重量、大小属性无法用于判别这些球。所以颜色这个属性就是我们需要记住的。同理,机器学习的是输入数据中的特征属性,并且这些属性需要有区分度,比如输入是图片,可以学习的特征属性就有颜色,边信息,空间结构信息等,同一类数据一般都有相同的特征,可以将它称作模式pattern。在我看来机器学习主要包括特征的提取、特征的匹配及相似度计算。更专业一点就是,从训练数据中提取通用的信息,并基于这些信息在位置数据上进行决策。
监督式分类
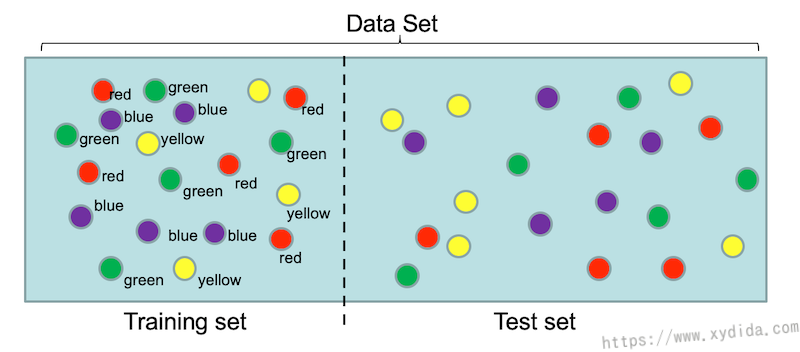
训练数据被人为标注上了正确的分类,训练过程就是观察这些训练数据的特征,总结成规则,再将规则应用到测试数据集上,注意,测试时不能使用训练的数据。监督式就像一个老师带着学生学习,测试集就像试卷,平时接触不到。
非监督式分类
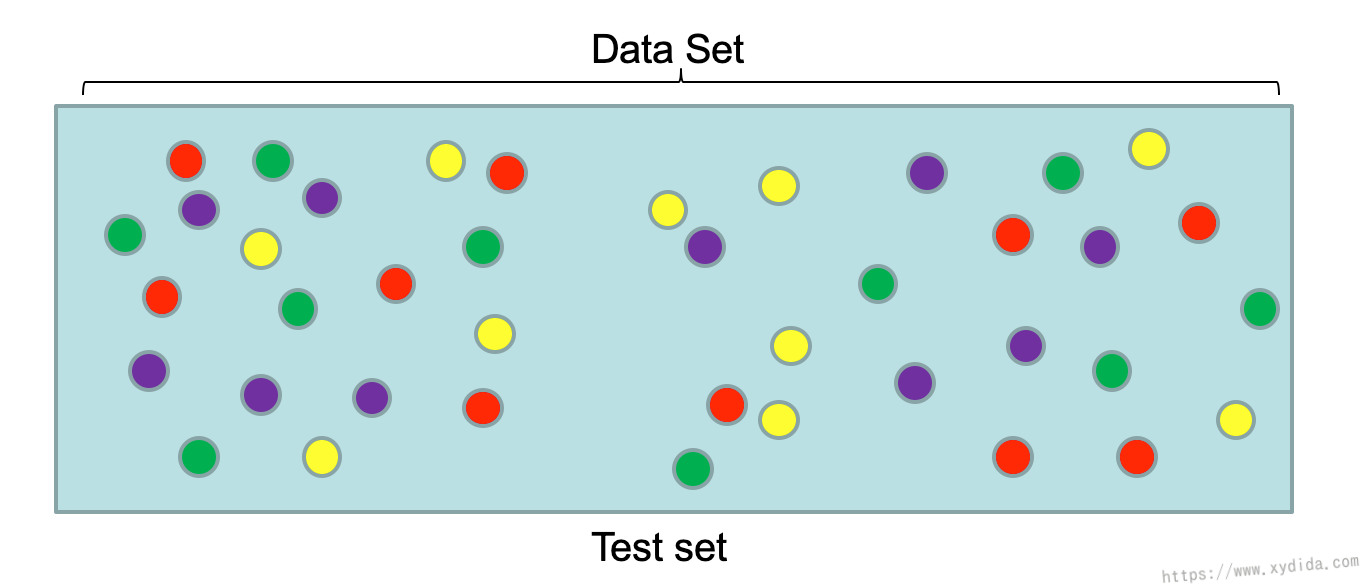
非监督式分类的训练数据和测试数据一样,没有标签,相对来说更难一点。机器学习系统根据数据的差异特征学习分类。
结果评估 Evaluation
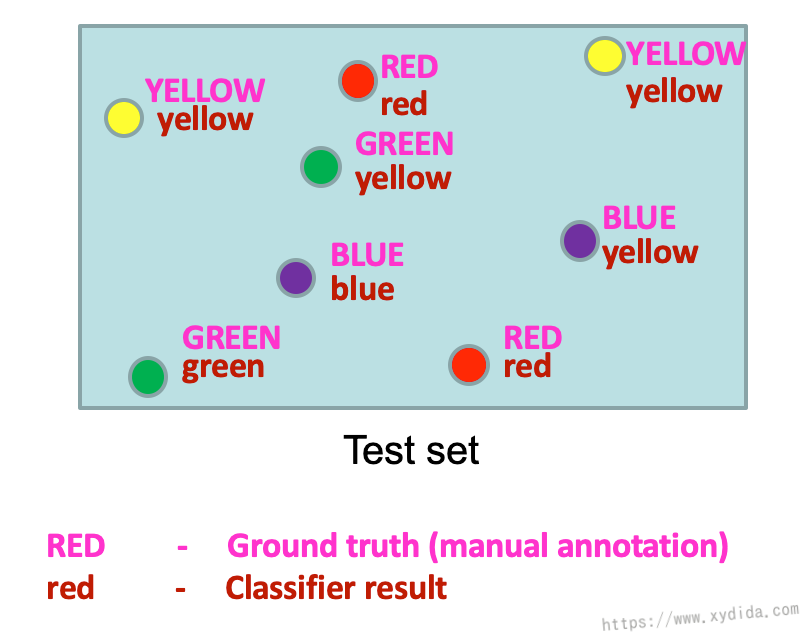
对于分类器做出的结果,如何评价呢?可以给测试数据集打上正确的分类标签(Ground Truth),再用测试数据跑一遍分类器,将预测结果和真实的分类标签比较,比较的方式靠计算数据之间的距离,两个靠得近,说明相似,分类效果就好,反之效果不好。
Confusion Matrix
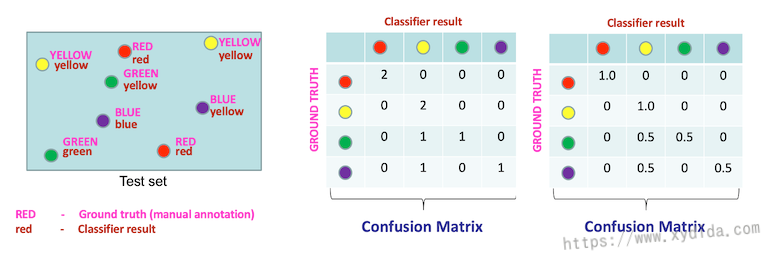
Confusion Matrix通常用来统计各个分类预测的频率,可以看出哪些分类机器预测的好,哪些预测的不好。表格中每一行代表真实的分类,每一列代表预测的分类,我们对每一行进行归一化处理,如果预测结果是正确的,归一化后就是1,数值越小,正确预测就越低。上图中绿色和紫色的精确度只有50%,绿色和紫色都容易被识别成黄色。表格中的对角线数值就是该分类下的准确度。对每一个分类的精度求一个平均就是Mean Average Precision (MAP),MAP代表了整体的精度,比如上图中的MAP值为:
Overfitting

Overfitting是训练中常常会遇到的一个难题,在训练时,往往会追求更高的精确度,这就导致模型学习该训练集下更多的特征,其中就包括了一些无用的特征,因为这些特征只对当前数据有用,换一个新的数据就起不到辨别的作用,总结下来就是模型的通用性(generalization)不强,死记硬背了很多特征。就好比考试,平时做题只背答案,习题集上都是满分,可一考试都不会,因为这些题都没见过呀。Overfitting在测试时的反应就是错误率很高,训练时的错误率很低。
Underfitting

和Overfitting相对应的就是Underfitting,这是因为模型太通用了,只学习到少量通用的特征,需要加强学习更多的模式和特征。Underfitting的表现就是错误率一直很高下不来。
Feature Space
特征空间(Feature Space)指从输入数据中提取的不同维度的特征构成的多维空间,比如,冰淇淋销量和对应当天空气湿度的数据,销量和空气湿度就构成一个二维平面特征空间,每一条记录映射到特征空间就是一个点。对于具有相同属性的数据,这些点会靠的很近。如何提取数据中的特征,很值得考究,特征多,模型就过于复杂,特征少,又不够充分表示对应的类别。
计算距离
对于监督式方法,判断模型预测的好坏就是计算预测值与真实值之间的距离,计算距离的方式有很多,比如L1,L2,马氏距离等。
L2距离
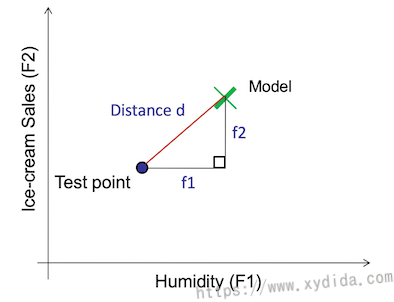
L2距离又称欧氏距离,可以解释为连接两个点的线段的长度。在二维空间中,公式如下:
三维空间:
推广到n维空间:
L2距离并不是尺度不变的,意味着计算的距离会根据特征的单位发生倾斜,在计算前,通常会将数值归一化。但是,随着数据维数增加,会造成维数灾难(curse of dimension)。
L1距离
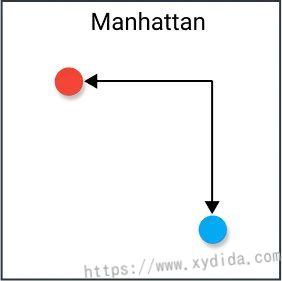
L1距离又称曼哈顿距离、出租车距离、城市距离,计算公式如下: