Reading notes on Interpolating between Optimal Transport and MMD using Sinkhorn Divergences
The purpose of this paper is to show that the Sinkhorn divergences are convex, smooth, positive definite loss functions that metrize the convergence in law.
Countless methods in machine learning and image processing reley on comparisons betwen probability distributions. But simple dissimilarities such as the Total Variation norm or the Kullback-Leibler relative entropy do not take into account the distance d on the feature space . As a result, they do not metrize the convergence in law and are unstable with respect to deformations of the distributions’ support. Optimal Transport distances (sometimes refeered as Earth Mover’s Distance) and Maximum Mean Discrepancies are continuous with respect to convergence in law and metrize its topology when feature space is compact.
OT distances and entropic regularization
Optimal Transportation (OT) costs are used to measure the geometric distances. They are computed as solutions of a linear program. However, in practice, solving the linear problem required to compute these OT distances is a challenging issue; many algorithms that leverage the properties of the underlying feature space (, d) have thus been designed to accelerate the computations. entropic regularization has recently emerged as a computationally efficient way of approximating OT costs.
MMD norms
To define geometry-aware distances between measures, a simpler approach is to integrate a positive definite kernel k(x; y) on the feature space . On a Euclidean feature space, RBF kernels such as the Gaussian kernel or energy distance kernel are used. Such Euclidean norms are often referred to as “Maximum Mean Discrepancies (MMD)”. MMD norms are cheaper to computer that OT and have a smaller sample complexity.
Interpolation between OT and MMD using Sinkhorn divergences
In sharp contrast, MMD norms rely on convolutions with a (Green) kernel and mimic electrostatic potentials. They observe vanishing gradients next to the extreme points of the measures’ supports.
On the one hand, losses have appealing geometric properties; on the other hand, cheap MMD norms scale up to large batches with a low sample complexity. Jean Feydy et,al consider a new cost built from that called Sinkhorn divergences:
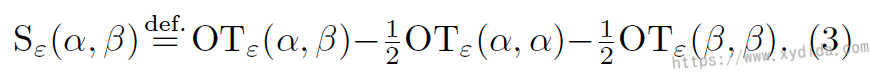
Computing the Sinkhorn divergence
Sinkhorn divergence can be implemented: use the Sinkhorn iterations to compute cross-correlation dual vectors, use the
symmetric Sinkhorn update to compute the autocorrelation dual vectors. The Sinkhorn loss can be computed:
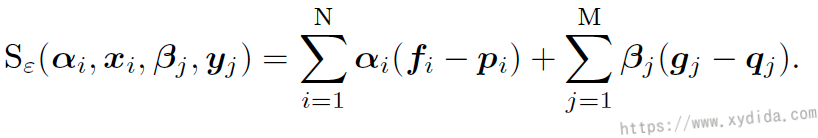
results
